メモ帳ブログ @ wiki
フーリエ級数展開
最終更新:
nina_a
-
view
フーリエ級数展開
目次
概要
フーリエ級数展開とは、『複雑な波形でも単純な波形の合成によっている』という考え方を利用して、ある波形を三角関数(サインとコサイン)のみを用いて表すことをいう。
周期 の関数
の関数 は以下のように表現できる。
は以下のように表現できる。
周期
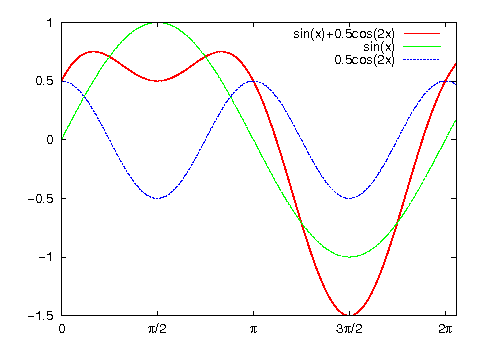
図・単純な波形の組み合わせによって構成されている波形(EPS)
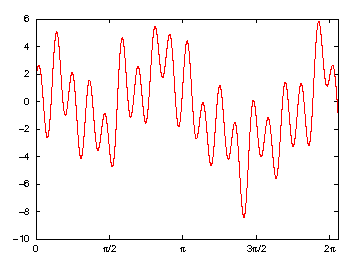
図・複雑な波形(EPS)
参考例
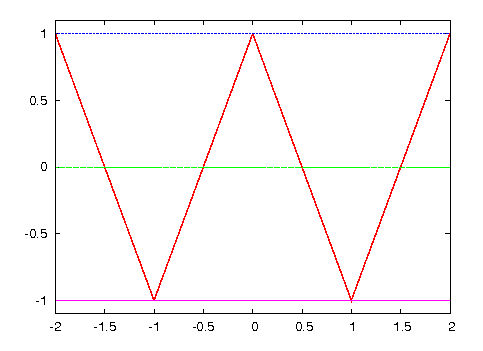
図・フーリエ級数展開する関数
結果は、


となる。
となる。
※途中計算については解説内の参考例に記してある。
計算機上では無限大までの和を求めることは出来ないため、途中で計算を打ち切ることになる。
n=5で打ち切った場合のグラフは以下のようになる。
n=5で打ち切った場合のグラフは以下のようになる。
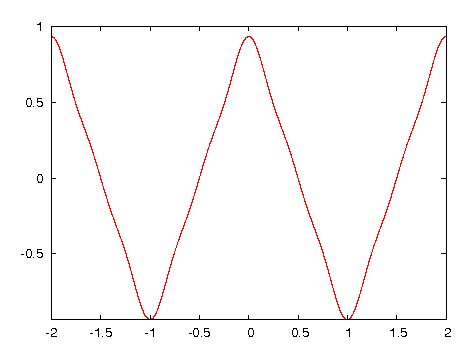
図・フーリエ級数展開した結果(n=5で打ち切り)(EPS)
n=25で打ち切った場合のグラフは以下のようになる。
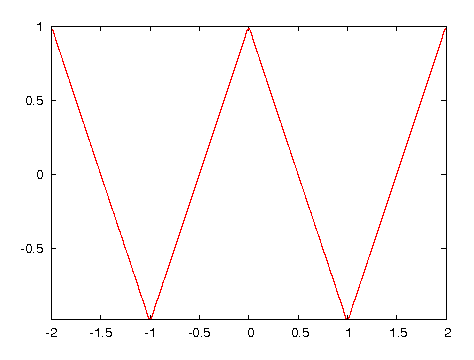
図・フーリエ級数展開した結果(n=25で打ち切り)(EPS)
解説
『任意の周期信号は、直流成分(いわば平均)と基本波成分と高調波成分(基本波の周波数を定数倍した物)の和から構成される。すなわち、
(任意の周期信号)=(直流成分)+(基本波成分)+(2倍高調波成分)+(3倍高調波成分)+…
が成り立つ。
フーリエ級数展開では基本波として正弦波と余弦波を用いる。よって、フーリエ級数展開は以下のように表される。
フーリエ級数展開では基本波として正弦波と余弦波を用いる。よって、フーリエ級数展開は以下のように表される。
※フーリエ級数展開において(私の身の回りでは)横軸に時間tを取ることが多いため以降の説明では変数としてtを用いる。
なお、 とは基本角周波数(基本波の角周波数の意、角周波数は角速度とも言う)であり、
とは基本角周波数(基本波の角周波数の意、角周波数は角速度とも言う)であり、 である。同様に、
である。同様に、 は基本周期、
は基本周期、 は基本周波数であり、
は基本周波数であり、 である。
である。
※ という関係は、フーリエ級数展開する関数の周期と基本波の周期の関係から導出される。
という関係は、フーリエ級数展開する関数の周期と基本波の周期の関係から導出される。
tが0から まで一周期分変化するとき、基本波
まで一周期分変化するとき、基本波 と
と も一周期分変化する必要がある。
も一周期分変化する必要がある。
tが0から
だから、 であることが分かる。
であることが分かる。
図・周期 の波と基本正弦波
の波と基本正弦波
※この関数列が本当に直交系を成しているかどうかの確認は省略する。偶関数、奇関数の性質を利用すれば容易に証明可能である。
直交関数系の性質を用いると、 、
、 、
、 を綺麗に求めることが出来る。実際に
を綺麗に求めることが出来る。実際に と
と の内積を取ると下図のようになり、
の内積を取ると下図のようになり、 の項のみ残り、他の項は全て0になる。
の項のみ残り、他の項は全て0になる。

上図から となる。同様にして
となる。同様にして と
と の内積から
の内積から が、
が、 と
と の内積から
の内積から が求められる。それぞれ以下のようになる。
が求められる。それぞれ以下のようになる。


内積の定義からこれを積分で表し、計算可能な所を計算すると、概要で示した式が得られる。
※ここでは内積の計算結果のみ記しておく。



なお、フーリエ級数展開は以下のように書かれることもある。
※上記の式は定数関数1を と見なして表した物である。
と見なして表した物である。
参考例
概要の参考例として扱った関数 のフーリエ級数展開の計算過程をここに記す。
のフーリエ級数展開の計算過程をここに記す。

図・フーリエ級数展開する関数(再掲)
図から、周期は2であることが分かる。
つづいて、 は、
は、

 は偶関数であるから
は偶関数であるから

![=\frac{2}{n\pi}\left[(2x+1)\sin(n\pi x)\right]_{-1}^0-\frac{4}{n\pi}\int_{-1}^0\sin(n\pi x)\,\mathrm{dx}](http://chart.apis.google.com/chart?cht=tx&chf=bg,s,ffffff00&chco=000000ff&chs=25&chl=%3D%5Cfrac%7B2%7D%7Bn%5Cpi%7D%5Cleft%5B%282x%2B1%29%5Csin%28n%5Cpi%20x%29%5Cright%5D_%7B-1%7D%5E0-%5Cfrac%7B4%7D%7Bn%5Cpi%7D%5Cint_%7B-1%7D%5E0%5Csin%28n%5Cpi%20x%29%5C%2C%5Cmathrm%7Bdx%7D)
![=0-\frac{4}{n^2\pi^2}\left[-\cos(n\pi x)\right]_{-1}^0](http://chart.apis.google.com/chart?cht=tx&chf=bg,s,ffffff00&chco=000000ff&chs=25&chl=%3D0-%5Cfrac%7B4%7D%7Bn%5E2%5Cpi%5E2%7D%5Cleft%5B-%5Ccos%28n%5Cpi%20x%29%5Cright%5D_%7B-1%7D%5E0)

複素指数関数表現によるフーリエ級数展開
複素指数関数とは底がネイピア数 であり、指数が虚数である関数
であり、指数が虚数である関数 である。
である。
複素指数関数のマクローリン展開から以下の関係が導かれる。

複素指数関数のマクローリン展開から以下の関係が導かれる。
※この計算については省略する。
ここでcis関数を以下のように定義する。

すなわち である。
である。
この定義から、

であることが分かる。これをフーリエ級数展開の式に代入し整理する(下図)。
すなわち
この定義から、
であることが分かる。これをフーリエ級数展開の式に代入し整理する(下図)。
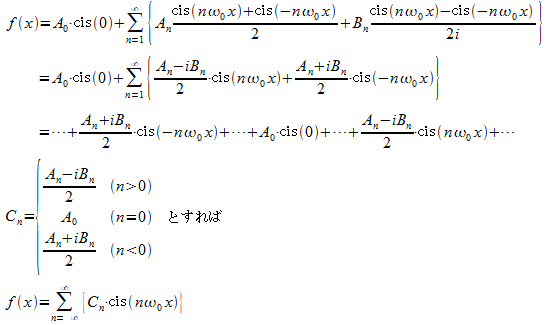
図・複素指数関数をフーリエ級数展開に適用(EPS)
これで複素指数関数によりフーリエ級数展開を表現する事が出来た。

三角関数による表現よりも簡潔になっていることが分かる。ただ がごちゃごちゃしているので、それぞれ計算してみる。
がごちゃごちゃしているので、それぞれ計算してみる。
1) n>0の時




2) n=0の時


3) n<0の時



三角関数による表現よりも簡潔になっていることが分かる。ただ
1) n>0の時
2) n=0の時
3) n<0の時
これらより、


となる。
以上をまとめると、複素指数関数を用いたフーリエ級数展開は、
となる。
以上をまとめると、複素指数関数を用いたフーリエ級数展開は、
となり、三角級数に比べるとかなり簡単に記述が可能である。
※ただし、 は奇関数でも偶関数でもないため、手計算の場合は計算が面倒になる場合がある。
は奇関数でも偶関数でもないため、手計算の場合は計算が面倒になる場合がある。
方形波のフーリエ級数展開
下図のような方形波のフーリエ級数展開を行う。
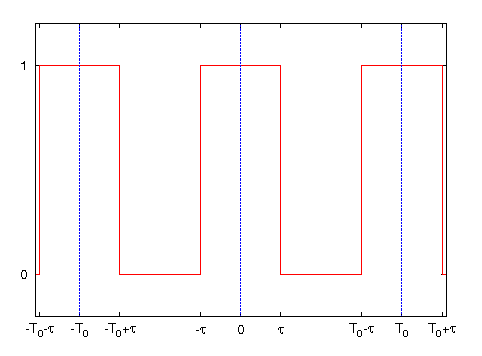
図・方形波(EPS)
まず、直流成分は



続いて、n倍高調波成分は





続いて、n倍高調波成分は
※cis関数の微分・積分


以上より方形波のフーリエ級数展開係数は、

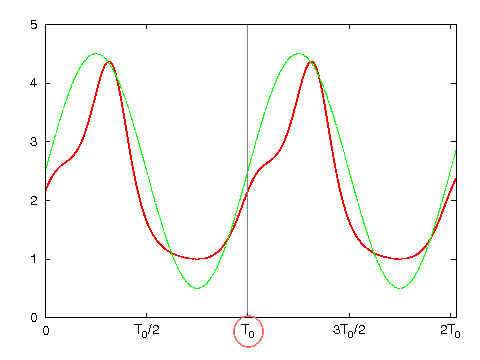
となった。方形波は無限倍の高調波成分まで含まれるため、計算機上ではある所までの高調波までで打ち切ることになる。打ち切り時に誤差が生じる現象をギプス現象という。もちろん、高い周波数成分まで加算した方がギプス現象は小さくなる。
となった。方形波は無限倍の高調波成分まで含まれるため、計算機上ではある所までの高調波までで打ち切ることになる。打ち切り時に誤差が生じる現象をギプス現象という。もちろん、高い周波数成分まで加算した方がギプス現象は小さくなる。
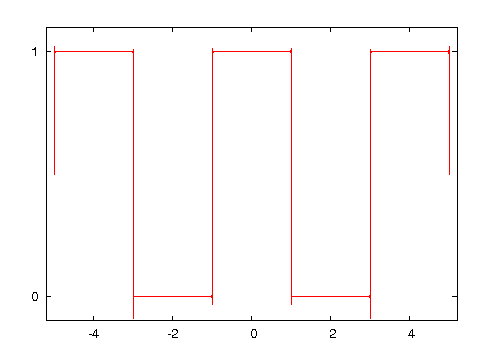
図・10000倍高調波までの加算( とした)(EPS)
とした)(EPS)
周波数スペクトル
上で得られたフーリエ級数展開係数 を図示すると以下のようになる。なお、下図には関数
を図示すると以下のようになる。なお、下図には関数 も一緒に図示した。
も一緒に図示した。

図・フーリエ級数展開係数(EPS)
上の図は各周波数成分がどれだけ含まれているかを示している。このような図を周波数スペクトル、あるいは、単にスペクトルという。
カテゴリ:MISC


